Program On Tower Of Hanoi
This problem can easily solved for small values of n. However, the level of difficulty increases rapidly as the number of disks increases.
Tower Of Hanoi Math Is Fun
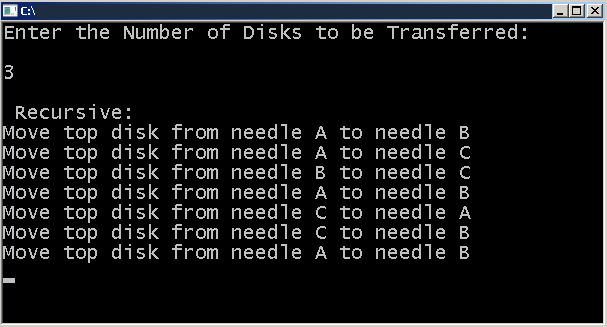
It is also very difficult to write a program for this problem using loops and other control structures. However, the use of recursion leads to a very simple and elegant solution.The first step in implementing recursion is to find out how we can reduce the size of the problem under consideration. The problem of moving n disks, can be decomposed into smaller problems of moving n - 1 disks as shown below:1. Move n - I disks from the source pole to the intermediate pole2. Move remaining disk from the source pole to the target pole. Move n -1 disks from the intermediate pole to the target pole.The second step is to decide the terminating condition. Note that the problem of moving n – 1 disks in steps l and 3 will actually be solved in terms of the smaller problem of moving n – 2 disks, which in turn will be solved in terms of the still smaller problems involving n - 3 disks and so on for as long as there is at least one disk to be moved.
Thus, the terminating condition for this problem is that the number of disks to be moved should be equal to zero.The complete program that includes a recursive function hanoiis given below. The function accepts four parameters. The parameter ndisk of type int specifies the number of disks to be moved. The other three parameters, namely, source, target and other, are of type char and specify a single character identification of the source, target and intermediate poles, respectively./. Tower of Hanoi program./.
Tower of Hanoi, is a mathematical puzzle which consists of three towers (pegs) and more than one rings is as depicted −These rings are of different sizes and stacked upon in an ascending order, i.e. The smaller one sits over the larger one.
There are other variations of the puzzle where the number of disks increase, but the tower count remains the same. RulesThe mission is to move all the disks to some another tower without violating the sequence of arrangement. A few rules to be followed for Tower of Hanoi are −.
Only one disk can be moved among the towers at any given time. Only the 'top' disk can be removed. No large disk can sit over a small disk.Following is an animated representation of solving a Tower of Hanoi puzzle with three disks.Tower of Hanoi puzzle with n disks can be solved in minimum 2 n−1 steps. This presentation shows that a puzzle with 3 disks has taken 2 3 - 1 = 7 steps. AlgorithmTo write an algorithm for Tower of Hanoi, first we need to learn how to solve this problem with lesser amount of disks, say → 1 or 2. We mark three towers with name, source, destination and aux (only to help moving the disks).
Recursive Program Tower Of Hanoi
If we have only one disk, then it can easily be moved from source to destination peg.If we have 2 disks −. First, we move the smaller (top) disk to aux peg. Then, we move the larger (bottom) disk to destination peg. And finally, we move the smaller disk from aux to destination peg.So now, we are in a position to design an algorithm for Tower of Hanoi with more than two disks. We divide the stack of disks in two parts. The largest disk (n th disk) is in one part and all other (n-1) disks are in the second part.Our ultimate aim is to move disk n from source to destination and then put all other (n1) disks onto it. We can imagine to apply the same in a recursive way for all given set of disks.The steps to follow are − Step 1 − Move n-1 disks from source to aux Step 2 − Move n th disk from source to dest Step 3 − Move n-1 disks from aux to destA recursive algorithm for Tower of Hanoi can be driven as follows −STARTProcedure Hanoi(disk, source, dest, aux)IF disk 1, THENmove disk from source to destELSEHanoi(disk - 1, source, aux, dest) // Step 1move disk from source to dest // Step 2Hanoi(disk - 1, aux, dest, source) // Step 3END IFEND ProcedureSTOPTo check the implementation in C programming,.